Operácie s maticami
| Site: | E-learning Pedagogickej fakulty KU |
| Course: | Učebné materiály z diskrétnej matematiky |
| Book: | Operácie s maticami |
| Printed by: | Guest user |
| Date: | Friday, 13 March 2026, 11:03 PM |
Description
Kapitola Operácie s maticami zahŕňa:
- rovnosť matíc
- súčet matíc
- násobok matice
- súčin matíc
1. Rovnosť matíc
Hovoríme, že matice A = \( \parallel a_{ij}\parallel \), B = \( \parallel b_{ij}\parallel \) typu m × n sa rovnajú, ak pre i = 1, 2, ..., n je aij = bij.
Príklad:
Dané sú matice A, B, C:
$$ A = \left(\begin{array}{ccc} 2&4 \\ 0&-2\end{array}\right) ,\ B = \left(\begin{array}{ccc} 2&\sqrt{16} \\ \mathrm{log} \ 1&-2\end{array}\right) ,\ C = \left(\begin{array}{ccc} 2&4 \\ 0&-2 \\ 0&0\end{array}\right) $$
\( A = B \), pretože $$ \left(\begin{array}{ccc} 2&4 \\ 0&-2\end{array}\right) = \left(\begin{array}{ccc} 2&\sqrt{16} \\ \mathrm{log} \ 1&-2\end{array}\right) $$
\( A \neq C \), pretože $$ \left(\begin{array}{ccc} 2&4 \\ 0&-2\end{array}\right) \neq \left(\begin{array}{ccc} 2&4 \\ 0&-2 \\ 0&0\end{array}\right) $$
2. Súčet matíc
Súčtom matíc A = \( \parallel a_{ij}\parallel \), B = \( \parallel b_{ij}\parallel \) typu m × n rozumieme maticu C = \( \parallel c_{ij}\parallel \) typu m × n, kde cij = aij + bij pre i = 1, 2, ..., m; j = 1, 2, ..., n.
Príklad:
Vypočítajte súčet matíc A + B, ak $$ A+B = \left(\begin{array}{ccc} 2&1&-3 \\ 1&-2&4\end{array}\right) + \left(\begin{array}{ccc} 5&3&-3 \\ 1&2&-6\end{array}\right)$$
riešenie:
$$ A+ B = \left(\begin{array}{ccc} 2&1&-3 \\ 1&-2&4\end{array}\right) + \left(\begin{array}{ccc} 5&3&-3 \\ 1&2&-6\end{array}\right) = \left(\begin{array}{ccc} 2+5&1+3&-3-3 \\ 1+1&-2+2&4-6\end{array}\right) = \left(\begin{array}{ccc} 7&4&-6 \\ 2&0&-2\end{array}\right)$$
3. Násobok matice
Násobkom matice A = \( \parallel a_{ij}\parallel \) typu m × n číslom α rozumieme maticu B = \( \parallel b_{ij}\parallel \) typu m × n, kde bij = α . aij pre i = 1, 2, ..., m; j = 1, 2, ..., n.
V prípade α = –1 maticu B nazývame opačnou maticou k matici A.
Príklad:
Vypočítajte násobok matice α.A, ak α = 2 a matica $$ A = \left(\begin{array}{ccc} 2&1&-3 \\ 1&-2&4\end{array}\right) $$
riešenie:
$$ \alpha.A = 2.A = 2 . \left(\begin{array}{ccc} 2&1&-3 \\ 1&-2&4\end{array}\right) = \left(\begin{array}{ccc} 2.2&2.1&2.(-3) \\ 2.1&2.(-2)&2.4\end{array}\right) = \left(\begin{array}{ccc} 4&2&-6 \\ 2&-4&8\end{array}\right) $$
4. Súčin matíc
Súčinom matíc A = \( \parallel a_{ij}\parallel \) typu m × p a B = \( \parallel b_{ij}\parallel \) typu p × n rozumieme maticu C = \( \parallel c_{ij}\parallel \) typu m × n kde 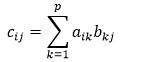

Veta: Pre ľubovoľné matice A = \( \parallel a_{ij}\parallel \) typu m × n, B = \( \parallel b_{ij}\parallel \) typu n × p, C = \( \parallel c_{ij}\parallel \) typu n × p a D = \( \parallel d_{ij}\parallel \) typu p × r, jednotkové a nulové matice Em, En, Om×n, Op×r, Om×p, On×r a ľubovoľné čísla α, β platí:
- A(BD) = (AB)D
- (B + C)D = BD + CD
- A(B + C) = AB + AC
- α(βA) = (αβ)A
- α(AB) = (αA)B = A(αB)
- Em A = A = A En
- Om×n + A = A + Om×n
- Om×n B = Om×p
Príklad:Zistite, či existujú súčiny A . B a B . A a ak áno, tak ich vypočítajte, kde $$ A = \left(\begin{array}{ccc} 1&2 \\ 3&4 \\ 5&6\end{array}\right) \ B = \left(\begin{array}{ccc} -1&-2 \\ -3&-4\end{array}\right). $$
riešenie:Matica A je typu 3×2, matica B typu 2×2. Počet stĺpcov matice A je rovný počtu riadkov matice B, teda súčin A . B existuje. Výsledná matica je typu 3×2. Teda $$ A.B = \left(\begin{array}{ccc} c_{11}&c_{12} \\ c_{21}&c_{22} \\ c_{31}&c_{32}\end{array}\right) = \left(\begin{array}{ccc} -7&-10 \\ -15&-22 \\ -23&-34\end{array}\right)$$
\( c_{11} = \left(\begin{array}{ccc} 1&2\end{array}\right) . \left(\begin{array}{ccc} -1 \\ -3\end{array}\right) = 1.(-1)+2.(-3)=-7 \)
\( c_{12} = \left(\begin{array}{ccc} 1&2\end{array}\right) . \left(\begin{array}{ccc} -2 \\ -4\end{array}\right) = 1.(-2)+2.(-4)=-10 \)
\( c_{21} = \left(\begin{array}{ccc} 3&4\end{array}\right) . \left(\begin{array}{ccc} -1 \\ -3\end{array}\right) = 3.(-1)+4.(-3)=-15 \)
\( c_{22} = \left(\begin{array}{ccc} 3&4\end{array}\right) . \left(\begin{array}{ccc} -2 \\ -4\end{array}\right) = 3.(-2)+4.(-4)=-22 \)
\( c_{31} = \left(\begin{array}{ccc} 5&6\end{array}\right) . \left(\begin{array}{ccc} -1 \\ -3\end{array}\right) = 5.(-1)+6.(-3)=-23 \)
\( c_{32} = \left(\begin{array}{ccc} 5&6\end{array}\right) . \left(\begin{array}{ccc} -2 \\ -4\end{array}\right) = 5.(-2)+6.(-4)=-34 \)
Súčin B . A nie je definovaný (počet stĺpcov matice B nie je rovný počtu riadkov matice A).
