Inverzná matica
| Portál: | E-learning Pedagogickej fakulty KU |
| Kurz: | Učebné materiály z diskrétnej matematiky |
| Kniha: | Inverzná matica |
| Vytlačil(a): | Hosťovský používateľ |
| Dátum: | piatok, 13 marca 2026, 19:51 |
Opis
Kapitola je zameraná na určenie hodnosti matice a nájdenie inverznej matice.
1. Hodnosť matice
Hodnosťou matice A, označujeme h(A), nazývame počet nenulových riadkov stupňovitej matice, ktorá je s maticou A riadkovo ekvivalentná.
Všetky stupňovité matice riadkovo ekvivalentné s danou maticou majú rovnaký počet nenulových riadkov.
Ukážeme si postup, ako určíme hodnosť konkrétnej matice. Pri určovaní hodnosti matice používame elementárne riadkové úpravy dovtedy, kým maticu neupravíme na tzv. trojuholníkový tvar. Je to taký tvar matice, pri ktorom:
- Ak aij a akl sú dva vedúce prvky riadkov (vedúci prvok riadku je prvý nenulový prvok riadku) a i < k, potom j < l. (t.j. “vedúce prvky sú usporiadané v riadkoch sprava doľava“)
- Pod vedúcimi prvkami riadkov sa nachádzajú iba nulové prvky.
$$ A = \left(\begin{array}{ccc} 1&2&3 \\ 0&2&1 \\ 0&0&2\end{array}\right)\ B = \left(\begin{array}{ccc} 1&2&3 \\ 0&0&1 \\ 0&0&0\end{array}\right)\ C = \left(\begin{array}{ccc} 1&2&3&-1&0 \\ 0&0&2&3&-1 \\ 0&0&0&1&2\end{array}\right)\ D = \left(\begin{array}{ccc} 1&2&-1 \\ 0&1&3 \\ 0&0&7 \\ 0&0&0\end{array}\right)$$
Hodnosť matice potom určíme tak, že spočítame počet nenulových riadkov trojuholníkovej matice. Teda hodnosť matice A je 3, čo zapisujeme h(A)=3. Podobne, h(B)=2, h(C)=3, h(D)=3.
2. Inverzná matica
Hovoríme, že matica B je inverznou maticou k štvorcovej matici A n-tého stupňa, ak platí AB = BA = En.
Inverznú maticu značíme B = A-1.
Veta: Nech pre štvorcové matice A, B n-tého stupňa existujú inverzné matice A-1 , B-1 . Potom platí:
- (A-1)-1 = A
- (AB)−1 = B-1 A-1
- E-1 = E
Príklad:Nájdite inverznú maticu B k matici A, ak $$ A = \left(\begin{array}{ccc} 1&-1&0 \\ 2&2&1 \\ 0&3&1\end{array}\right) $$
riešenie:
Maticu A a jednotkovú maticu E3 napíšeme vedľa seba a pomocou elementárnych riadkových úprav maticu A upravíme na jednotkovú maticu, pričom tie isté úpravy vykonávame aj na matici E3.
Najprv maticu A (jej prvky sú zvýraznené tučným písmom) upravíme na stupňovitú maticu
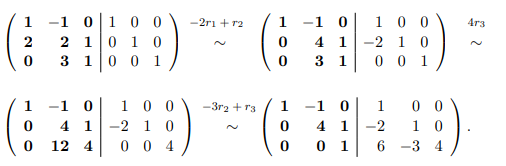
Ďalej postupujeme podobne, len úpravy vykonávame ”zdola nahor”.


Matica napravo od jednotkovej matice je hľadaná inverzná matica.
$$ B = A^{-1} = \left(\begin{array}{ccc} -1&1&-1 \\ -2&1&-1 \\ 6&-3&4\end{array}\right) $$