2. Inverzná matica

Hovoríme, že matica B je inverznou maticou k štvorcovej matici A n-tého stupňa, ak platí AB = BA = En.

Inverznú maticu značíme B = A-1.

Veta: Nech pre štvorcové matice A, B n-tého stupňa existujú inverzné matice A-1 , B-1 . Potom platí:

  1.  (A-1)-1 = A 
  2.  (AB)−1 = B-1 A-1 
  3.  E-1 = E
Príklad:

Nájdite inverznú maticu B k matici A, ak $$ A = \left(\begin{array}{ccc} 1&-1&0 \\ 2&2&1 \\ 0&3&1\end{array}\right) $$ 

riešenie:

Maticu A a jednotkovú maticu E3 napíšeme vedľa seba a pomocou elementárnych riadkových úprav maticu A upravíme na jednotkovú maticu, pričom tie isté úpravy vykonávame aj na matici E3.

Najprv maticu A (jej prvky sú zvýraznené tučným písmom) upravíme na stupňovitú maticu


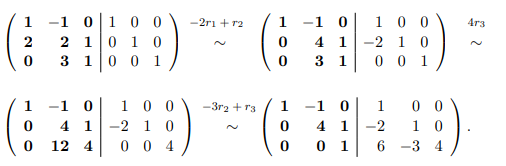
Ďalej postupujeme podobne, len úpravy vykonávame ”zdola nahor”.


Matica napravo od jednotkovej matice je hľadaná inverzná matica.
$$ B = A^{-1} = \left(\begin{array}{ccc} -1&1&-1 \\ -2&1&-1 \\ 6&-3&4\end{array}\right) $$